Prise en main de l'IDE Pyzo et du language Python

• Allumer l'ordinateur.
• Se connecter.
  • votre identifiant est de la forme prenom.nom sans accents
    • éventuellement tronqués au premier sous mot (avant tout - ou espace).
    • éventuellement de la forme p.nom, où p est la première lettre du prénom.
  • votre mot de passe est votre date de naissance, sous la forme jjmmaaaa.

Pyzo est un IDE (Integrated Development Environment : un logiciel qui regroupe plusieurs outils utiles au développement) pour la programmation en Python. C'est un logiciel libre.

1. Lancer l'application Pyzo

   

2. Pyzo détecte automatiquement un environnement Python préinstallé. Si nécessaire, cliquer sur le lien pour confirmer l'utilisation de cet environnement.

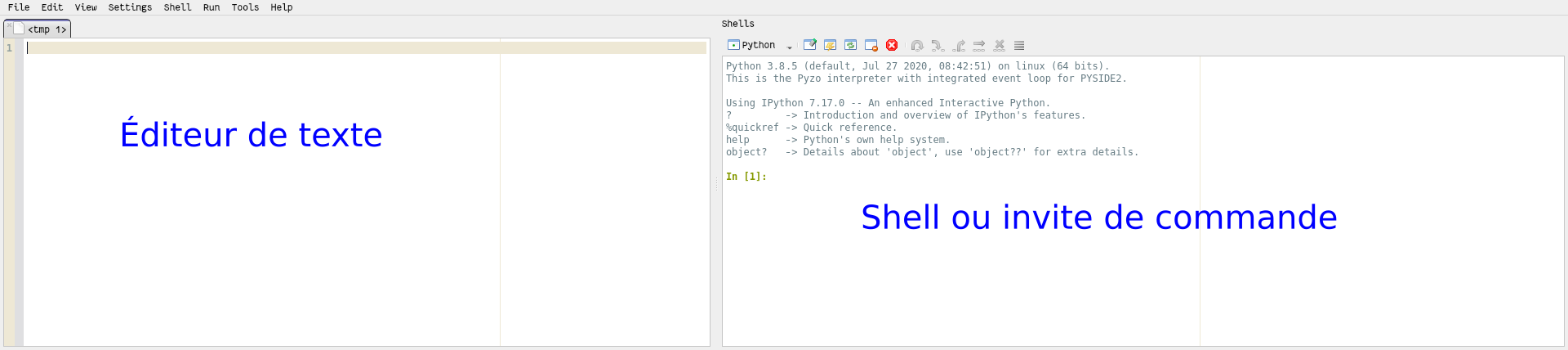
Le logiciel Pyzo présente plusieurs fenêtres. On n'utilisera que les deux fenêtres suivantes — fermer les autres.

• L'éditeur de texte interactif.
• Le shell, ou invite de commande. Sa fenêtre ressemble à la fenêtre de droite de la capture suivante. Selon la configuration, l'invite In [1]: du shell IPython peut être remplacée l'invite $\inv$ du shell de base.

3. (optionnel, utile pour cette séance) Configurer l'utilisation de IPython :
   • Dans le menu Shell, choisir Configuration des shells
   • Cocher Utilise IPython si disponible, puis Done.
   • Menu Shell > Redémarrer.

Ouvrir le fichier T:/travail/CPGE/MPSI3/ITC/00 Prise en main.py.

Celui-ci contient un squelette, à remplir pendant le TP.

Les objets manipulés ont un type, dont voici les plus élémentaires, et ce qu'ils représentent.

Autre type fondamental : les listes, comme [3, 2, 6, 4], qui représentent un tableau de valeurs.

Les opérateurs arithmétiques de base +, -, *, / sont définis en Python. On peut utiliser le shell comme une calculatrice.

Les variables en Python ne sont pas comme des variables en mathématiques, qui peuvent prendre n'importe quelle valeur. Une variable Python n'existe que lorsqu'elle a été définie en y mettant une valeur particulière, ce qu'on appelle l'affectation. Une variable Python est comme une case mémoire.

In [1]: a = 3 # Définition d'une variable a
              # le shell ne renvoie rien
In [2]: a * 2 # On utilise la variable
Out[2]: 6

In [3]: b = a+2

In [4]: a = a*a

In [5]: a
Out[5]: 9
In [6]: a+b
Out[6]: 14

Les instructions précédentes définissent une variable a, et lui affectent initialement la valeur $3$. Cette variable peut être utilisée dans les expressions suivantes, elle y est remplacée par sa valeur. L'instruction a=a*a réaffecte la valeur $9$ à la variable a.

Noter que les affectations ne renvoient rien : il n'y a pas de résultat (pas de Out).

Les entiers relatifs sont représentés en Python par le type int (pour integer). Contrairement à d'autres langages de programmation, le type int de Python permet de représenter des entiers arbitrairement grands.

En plus des opérations +,-,*, Python définit les opérateurs suivants.

In [1]: 42 % 10
Out[1]: 2

In [2]: 42 // 10
Out[2]: 4

In [3]: 3 ** 3
Out[3]: 27

La commande magique %time (ou timeit pour le shell en $\inv$) permet de mesurer le temps d'exécution. Dans l'exemple suivant, le calcul de $7^{2^{20}}$ prend 234 ms¹.

In [1]: a = 2 ** 20
In [2]: %time b = 7 ** a
CPU times: user 224 ms, sys: 10.1 ms, total: 234 ms
Wall time: 234 ms

# Syntaxe correspondant à l'autre shell.
>>> timeit 7**(2**20)
0.23074946599808754 seconds on average

Exécuter la commande import math pour importer le module math de Python. Ce module définit les fonctions mathématiques usuelles. Noter en particulier les fonctions math.sqrt (square root, pour racine carrée), math.log (logarithme), math.exp (exponentielle), math.floor (partie entière), ainsi que les constantes math.e et math.pi.

• On peut trouver une liste des fonctions du module en exécutant help(math).
• Vous pouvez obtenir la documentation d'une fonction en particulier en exécutant help(math.log). On peut y lire que cette fonction log peut prendre un deuxième argument facultatif donnant la base du logarithme. Par exemple log(2 ** 10, 2) renverra le logarithme en base $2$ de $2^{10}$, c'est-à-dire 10.0.
• Exécuter from math import sqrt permet d'utiliser la fonction sqrt sans le préfixe math. Exécuter from math import * importe toutes les fonctions du module math.

Dans l'éditeur de texte, recopier le code Python suivant. Il définit une fonction puiss_quatre qui prend un argument, noté x, et renvoie cet argument élevé à la puissance quatre, il définit également une variable e et calcule la puissance quatrième de $e$.

def puiss_quatre(x): # Définition d'une fonction nommée puiss_quatre
    b = x*x          # Affectation d'une variable intermédiaire
    return b*b       # La fonction renvoie b*b

e = 3                # Retour à l'indentation : en dehors de la fonction
print(puiss_quatre(e))

L'interpréteur Python ignore la fin des lignes à partir du symbole #. Cela permet d'annoter le code de commentaires, pour le lecteur.

Attention à la syntaxe. Pour définir une fonction :

1. Utiliser le mot clef def, suivi du nom de la fonction, puis de ses arguments, entre parenthèses.
2. Ne pas oublier les : à la fin de cette ligne.
3. Indenter les instructions appartenant au corps de la fonction.

L'indentation est insérée automatiquement (par le shell également) quand vous appuyez sur la touche Entrée depuis la ligne précédente qui termine par :. Pour modifier l'indentation, utiliser les touches Tab (ajoute de l'indentation) et Shift + Tab (retire de l'indentation), depuis le début de la ligne.

Une fois le code précédent recopié (sans les commentaires), appuyer sur Ctrl+Entrée (ou Cmd+Entrée) pour faire exécuter le code dans le shell. Dans le shell, la variable e et la fonction puiss_quatre sont alors définies et le résultat de l'instruction puiss_quatre(2) est affiché. Il est maintenant possible d'exécuter dans le shell la commande puiss_quatre(e) pour obtenir $3^{4}=81$.

Bien qu'il soit possible de définir cette fonction directement dans le shell, l'éditeur permet

• de sauvegarder votre code dans un fichier source .py
• de modifier/corriger le code écrit avant de le réévaluer, ou de le copier-coller plus facilement

y = x
# range(6) tourne 6 fois
for i in range(6):
    y = y + x

Il est possible de séparer le fichier source en «cellules», délimitées par des lignes commençant par ### — chaque cellule correspondant à un exercice par exemple. Le raccourci Ctrl+Entrée n'exécute que la cellule actuelle (où est le curseur).

La fonction print permet d'afficher un message, ou la valeur d'une variable.

def puiss_quatre(x):
    b = x*x    # Une variable intermédiaire, qui vaut x²
    print("La variable b vaut", b)     # Les deux arguments seront affichés, séparés d'un espace
    return b*b # On a b² = (x²)² = x⁴

Après évaluation du code précédent,

In [1]: puiss_quatre(3)
La variable b vaut 9
Out[1]: 81

# Extrait 1
def f(a,b):
    z = 2*a+b
    return z
x = f(1,2)
y = f(2,1)
print(x,y)

# Extrait 2
def f(a,b):
    z = 2*a+b
    return z
x, y = 1, 1 # x=1 et y=1
x = f(x,y)
y = f(x,y)
print(x,y)

# Extrait 3
def f(a,b):
    return a*b
x = 1
y = 2
z = f(y, f(y, f(x,y)))
print(z)

Les opérateurs de multiplications et divisions sont prioritaires sur l'addition et la soustraction, et réalisées de gauche à droite.

In [1]: 3 * 2 // 3 # (3 * 2) // 3
Out[1]: 2

Les opérations d'exponentiation sont réalisées de droite à gauche.

In [1]: 2 ** 3 ** 2
Out[1]: 512 # = 2⁹

On peut représenter un couple de valeurs ou de variables en utilisant x, y ou (x,y).

In [1]: a = (3, 7) # définition d'un couple
In [2]: a[0] # Le premier élément correspond à
             # l'indice 0
Out[2]: 3
In [2]: a[1] # Le second à l'indice 1
Out[2]: 7

# À partir de a, on peut récupérer les deux
# valeurs par destructuration
In [3]: x, y = a # affectation de deux variables
In [4]: x
Out[4]: 3
In [5]: y
Out[5]: 7

L'affectation par couple peut être utilisée pour initialiser plusieurs variables en une seule ligne, ou échanger les valeurs de deux variables.

In [1]: x, y = 5, 7 # x = 5 et y = 7
In [2]: x, y
Out[2]: (5, 7)

In [3]: x, y = y, x # Échange des valeurs de x,y
In [4]: x, y
Out[4]: (7, 5)

Attention il y a une différence entre une fonction prenant en argument un couple et une fonction avec deux arguments.

def f(x,y): # Deux arguments
    return x+y
f(1,2)

def g(c): # c est un couple
    return c[0] + c[1]
g((1,2))

Par défaut,

• toute variable définie à l'intérieur d'une fonction n'est pas accessible en dehors de la fonction. On dit que sa portée est locale.
• les variables définies en dehors d'une fonction sont accessibles à l'intérieur de la fonction, mais ne peuvent pas être réaffectées depuis l'intérieur de la fonction.

def f(a,b):
    # z est une variable locale
    z = a * b
    return z
f(1,2)
print(z) # Erreur : z non défini

# x est une variable globale
x = 2
def f(a):
    return a+x
print(f(3)) # Affiche 5

x = 2 # variable globale
def f(a,b):
    x = 3 # nouvelle variable locale
          # qui «cache» la globale
    return x
print(f(1,2), x) # Affiche 3, 2

Il est en fait possible de réaffecter une variable globale depuis l'intérieur d'une fonction, en la déclarant comme telle.

compteur = 0 # Compte le nb d'appels de f
def f():
    global compteur # On spécifie que le nom compteur utilise une portée globale
    compteur += 1
f(); f() # deux appels de f
print(compteur) # Affiche 2

Plutôt que de réaffecter une variable, certaines opérations peuvent modifier l'objet sous-jacent. Les types permettant ce genre d'opérations sont dits mutables. Les entiers et les flottants ne sont pas mutables, on ne peut que réaffecter des variables pointant vers une telle donnée. À l'intérieur d'une fonction, une telle réaffectation a une portée locale.

Les listes sont des objets mutables (contrairement aux chaînes de caractères). Une fonction peut donc modifier une liste qui lui est passée en argument.

x = 2
def f(a):
    a = a + 2 # Nouvelle affectation de la variable
              # locale a
f(x)
print(x) # Affiche 2, x n'a pas été modifiée

l = [1,2] # Une liste, un objet mutable
def modifie(li):
    li[0] = -1   # Modification de la liste li
    li.append(3) # Modification de la liste li
modifie(l); modifie(l)
print(l) # Affiche [-1, 2, 3, 3] : l a été modifiée